Fonction cryptographique de hachage

Dans un précédant article, Eban a déjà introduit le concept de chiffrement, et pour reprendre les termes du blog chiffrer.info (la petite piqure de rappelle, ON DIT CHIFFRER, c'était juste au cas où), le chiffrement se définit comme étant "un procédé de cryptographie grâce auquel on souhaite rendre la compréhension d’un document impossible à toute personne qui n’a pas la clé de (dé)chiffrement". Très bien, mais parfois, on souhaite précisément qu'il ne soit pas possible d'effectuer l'opération de déchiffrement, par exemple dans le cas du stockage d'un mot de passe. C'est l'idée qui se cache derrière le hachage.

Notations et mathématiques

Vous le savez sûrement, tout ce qui concerne la cryptographie repose lourdement sur la mathématique, ainsi, je préfère préciser au préalable les notations que j'utiliserais et définir les différents objets que j'aurais à manipuler. À noter cependant qu'il n'est pas nécessaire de comprendre tout le contenu mathématique de l'article pour en comprendre l'essentiel, les détails présent sont simplement ici pour satisfaire les curieux (ou les matheux).

Au sujet des symboles et notations:

• $\in$ désigne "appartient à".
• $:=$ désigne l'égalité de définition dont j'estime l'utilisation plus rigoureuse (pour ceux qui voudraient plus de détails, vous pouvez regarder cette vidéo d'El Jj).
• Le produit d'une famille $(a_i)_{1\leq i\leq n}$ sera noté $a_1 \times...\times a_n= \prod_{i=1}^{n}{a_i}$, il en va de même pour sa somme qui sera notée $a_1 + ... + a_n = \sum_{i=1}^n{a_i}$.
• Pour $n$ un entier, on notera la factorielle de $n$, $1\times 2 \times ... \times n = \prod_{i=1}^{n}i = n!$.
• La notation $E^*$ désigne un ensemble de taille arbitraire, même infini.

Ce qui m'offre une super transition… Au sujet des objets ensemblistes:

• Un ensemble peut être définit de manière intuitive comme une collection d'objets, des nombres, des voitures, des matrices, ou des messages à chiffrer. Par convention, ils sont désignés par des lettres capitales.
• Si $E$ est un ensemble et $n$ un entier naturel non nul, $E^n = \{(x_1,...,x_n), x_{1\leq i\leq n} \in E\}$. Un élément de cet ensemble est appelé $n$-uplet de $E$. En d'autres termes, un $n$-uplet est une "suite" de $n$ éléments de $E$.
• On note, pour tout ensemble $E$, son cardinal noté $\text{Card}(E)$ (aussi $|E|$), se définit intuitivement comme l'entier naturel correspondant au nombre d'éléments de $E$.
• Une application $f$ est une relation entre deux ensembles $E$ et $F$ qui à tout élément $x\in E$, associe un élément $f(x) \in F$, on la note $f: E \rightarrow F$. On confondra volontairement les termes applications et fonctions.
• Prenons $x \in E$, $f(x)$ est appelée image, et $x$ antécédant. Pour coller au vocabulaire utilisé en cryptographie, un antécédant sera appelée préimage, et une image pourra être appelée condensat.
• Une fonction $f: E \rightarrow F$ est dite injective (est une injection) si et seulement si tout élément de $F$ admet au plus un antécédent par $f$.
• Une fonction $f: E \rightarrow F$ est dite surjective (est une surjection) si et seulement si tout élément de $F$ admet au moins un antécédent par $f$.

Au sujet de la logique booléenne:

• L'opération booléenne NOT sera notée $\neg$.
• L'opération booléenne AND sera notée $\wedge$.
• L'opération booléenne OR sera notée$\vee$.
• L'opération booléenne XOR sera notée $\oplus$.

Concept

On considère $M$ l'ensemble des messages possibles, une fonction de hachage $h$ peut se définir comme étant une fonctions de $M$ dans $H$, l'ensemble des images qui chacune possède une taille fixe $n$, un entier naturel. Cependant, il faut se rappeler que le message (et le condensat) sont en binaire, ils peuvent donc être écrit comme une suite de 0 et de 1 que l'on peut modéliser par un $n$-uplet de l'ensemble $\{0,1\}$. Ainsi, on peut prendre $M = \{0,1\}^*$ et $H = \{0,1\}^n$ (autrement dit, $h: \{0,1\}^* \rightarrow \{0,1\}^n$). Naturellement, une question peut venir à l'esprit. S'il s'agît d'une fonction, alors par définition je peux retrouver la préimage, ou au moins la calculer. Dans notre cas il s'agît d'un problème majeur pour la sécurité de l'algorithme. C'est pourquoi les fonctions de hachages se doivent d'être résistante à ce calcul de préimage. D'une autre manière, on fait en sorte que le calcul de $h(x)$ soit facile pour tout $x \in M$, et que pour tout $y \in H$, le calcul de $x \in M$ vérifiant $h(x) = y$ est long (oui c'est assez vague, mais la définition formelle est très complexe). Les fonctions de hachages sont appelées fonction à sens unique (ou One-Way function en anglais).

En fonction des caractéristiques de $h$, on lui donne des adjectifs spécifiques. En outre, on dira que $h$ est parfaite pour $M$ si elle est une injection de $M$ dans $H$ (en particulier, si de plus $\text{Card}(M) = \text{Card}(H)$, elle sera dite minimale). Un corolaire immédiat de cette définition est que si $h$ est parfaite, alors elle n'admet aucune collision (la preuve se tient à l'application de deux définitions, elle est donc laissée au soin du lecteur) c'est à dire des couples $(x,x') \in M^2, x\neq x'$ tels que $f(x) = f(x')$ (on peut minorer le nombre de collisions $c$, dans le cas où $M$ et $H$ sont finis: $c \geq \text{Card}(M) - \text{Card}(H)$) et on appelle seconde préimage $x'$. En revanche, cela paraît tout simplement impossible à obtenir, sans fixer l'ensemble $M$ ce qui risque d'entacher à la sécurité de $h$. Ainsi, le cas le plus fréquent sera de considérer une fonction de hachage qui est surjective, par conséquent, il existera toujours des collisions. Si $M$ est de taille infinie, c'est à dire s'il contient tout les messages imaginables, alors il y a une infinité de collisions possibles. Le but est désormais de pouvoir avoir une répartition homogène (statistiquement parlant, intuitivement cela signifie qu'il y en a un peu partout) de ces collisions. Nouvelle définition. On dit que $h$ est résistante aux collisions (ou Collision-Resistant Hash Function en anglais) si le calcul d'une collision est complexe calculatoirement (pour la même raison que que les One-Way-Function). Rendre une fonction résistante aux collisions est donc un objectif de sécurité important.

Je fais un petit aparté sur l'attaque des anniversaires. Le problème est simple, étant donné une population de $n$ individus, combien sont-ils nécessaires pour que la probabilité que deux aient la même date d'anniversaire soit supérieur à $\frac{1}{2}$. En effet, on peut assimiler cela, dans notre contexte, à la taille de l'ensemble des messages possibles pour que la probabilité d'avoir une collision soit supérieur à ladite probabilité. Avoir une connaissance de cette probabilité indique jusqu'à quel point une fonction cryptographique peut être résistante aux collisions.

L'explication qui suit repose énormément sur les mathématiques, et est uniquement présente pour expliquer plus en détail l'idée exposée, elle n'est pas essentielle pour la suite.

Soit $M = \{0,1\}^n$, pour chaque message possible. On souhaite approximer la probabilité que $p$ éléments aient la même image par $h$. Ainsi, il y a au total, $n^p$ possibilités. Si virtuellement on test chacune d'entre elles, on représente cela avec un arrangement: $A^p_n = \frac{n!}{(n-p)!}$ que l'on divise par le nombre totale de possibilités. En revanche, ici on à le cas où chacun à une image différente, donc l'évènement $X$ "au moins deux éléments ont leurs images identiques" a pour probabilité $\mathbb{P}(X) = 1 - \frac{n!}{(n-p)!n^p}$. On cherche alors à approximer ce résultat. Commençons par rappeler qu'au voisinage de $0$ (autrement dit très proche), on a $(1)~e^x = 1 + x + o(x)$ (où le $o(x)$ indique que le terme est négligeable en $0$, c'est à dire que quand $x$ tend vers $0$, $o(x)$ fait de même). Or à l'aide du produit il vient: $A^p_n = \frac{n!}{(n-p)!} = \prod_{k=n-p+1} ^{n}{k} = \prod_{j=0}^{p-1}{[j+n-p+1]}.$ Et en inversant ce dernier on obtient: $\prod_{j=0}^{p-1}[n-j].$ Mais: $\frac{1}{n^k} = \frac{1}{\prod_{j=0}^{n}n}.$ Finalement: $\frac{n!}{(n-p)!n^p} = \prod_{j=0}^{p-1}[n-j]\cdot\frac{1}{\prod_{j=0}^{p-1}n} = \prod^{p-1}_{j=0}\left[1-\frac{j}{n}\right]$. En reprenant $(1)$ il vient que: $\prod_{j=0}^{n}e^{-j/n} = \prod^{p-1}_{j=0}\left[1-\frac{j}{n} + o(j/n)\right].$ Soit que: $\mathbb{P}(X) \approx \prod_{j=0}^{n}e^{-j/n} =1- \exp\left(-\frac{1}{n}\sum_{j=0}^{p-1}j\right) = 1- \exp\left(-\frac{p(p-1)}{2n}\right).$ Cette approximation permet alors d'estimer le nombre de calculs nécessaires à un attaquant pour que la probabilité que deux messages forment une collision soit supérieure à $1/2$.

Condensat NT

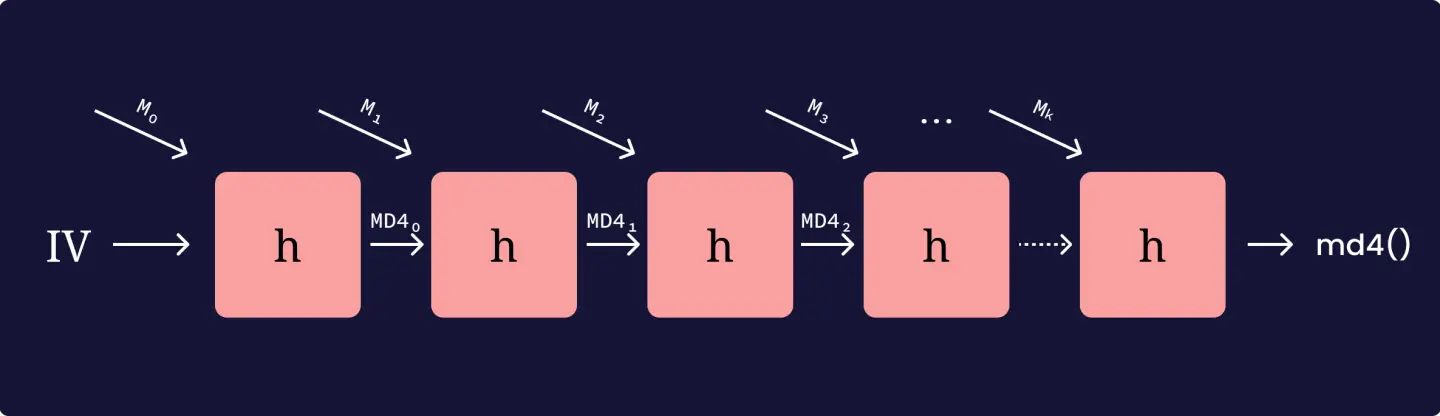
Dans la documentation de Microsoft officielle, les haches NT sont générés de la manière suivante (merci @Pixis d'ailleurs pour l'information): Define NTOWFv1(Passwd, User, UserDom) as MD4(UNICODE(Passwd)) Donc, c'est MD4 qui est utilisé (à noter que la fonction UNICODE() renvoie une chaîne encodée en UTF16-LE). Introduit en 1990 par Ronald Rivest, un cryptologue du MIT (surtout connu pour sa contribution à RSA), MD4 est décrit dans le RFC1320 (que vous pouvez trouver ici) et il se base sur la construction de Merkle-Damgård; c'est à dire qu'il emploie une fonction de compression. Le principe est assez simple: - On prend un message $M$ d'une certaine longueur. Puis on ajoute des zéros de telle sorte à ce que la longueur du message soit congrue à 448 modulo 512, plus formellement, $M \equiv 416 \mod 512$. - On divise le message en $k$ parties (pour être exact, $[k:=\text{len}(M)/16] \in \mathbb{N}$) de 16 bits (que l'on dénotera par la suite $(M_i)_{1\leq i \leq k}$). - On initialise 4 buffers $A:= \texttt{01 23 45 67}$, $B:= \texttt{89 ab cd ef}$, $C:= \texttt{fe dc ba 98}$, $D:= \texttt{76 54 32 10}$ (de bels séquences régulières n'est-ce pas ?). - On pose les fonctions suivantes de $(\{0,1\}^{32})^3 \rightarrow \{0,1\}^{32}$, $F(X,Y,Z):=(X \wedge Y) \vee (\neg X \wedge Z)$, $G(X,Y,Z):=(X \wedge Y) \vee (X \wedge Z) \vee (Y \wedge Z)$, $H(X,Y,Z):=X \oplus Y \oplus Z$. Ces fonctions agissent tels des fonctions de compressions sur les paramètres. - Enfin, on procède à un calcul itératif. Les calculs sont longs à décrire et assez similaire, donc je met le code issus de RFC:

    AA = A
    BB = B
    CC = C
    DD = D

    /* Round 1. */
    /* Let [abcd k s] denote the operation:
             a = (a + F(b,c,d) + X[k]) <<< s. */
    /* Do the following 16 operations. */
    [ABCD  0  3]  [DABC  1  7]  [CDAB  2 11]  [BCDA  3 19]
    [ABCD  4  3]  [DABC  5  7]  [CDAB  6 11]  [BCDA  7 19]
    [ABCD  8  3]  [DABC  9  7]  [CDAB 10 11]  [BCDA 11 19]
    [ABCD 12  3]  [DABC 13  7]  [CDAB 14 11]  [BCDA 15 19]

    /* Round 2. */
    /* Let [abcd k s] denote the operation:
             a = (a + G(b,c,d) + X[k] + 5A827999) <<< s. */
    /* Do the following 16 operations. */
    [ABCD  0  3]  [DABC  4  5]  [CDAB  8  9]  [BCDA 12 13]
    [ABCD  1  3]  [DABC  5  5]  [CDAB  9  9]  [BCDA 13 13]
    [ABCD  2  3]  [DABC  6  5]  [CDAB 10  9]  [BCDA 14 13]
    [ABCD  3  3]  [DABC  7  5]  [CDAB 11  9]  [BCDA 15 13]

    /* Round 3. */
    /* Let [abcd k s] denote the operation:
             a = (a + H(b,c,d) + X[k] + 6ED9EBA1) <<< s. */
    /* Do the following 16 operations. */
    [ABCD  0  3]  [DABC  8  9]  [CDAB  4 11]  [BCDA 12 15]
    [ABCD  2  3]  [DABC 10  9]  [CDAB  6 11]  [BCDA 14 15]
    [ABCD  1  3]  [DABC  9  9]  [CDAB  5 11]  [BCDA 13 15]
    [ABCD  3  3]  [DABC 11  9]  [CDAB  7 11]  [BCDA 15 15]

    /* Then perform the following additions. (That is, increment each
       of the four registers by the value it had before this block
       was started.) */
    A = A + AA
    B = B + BB
    C = C + CC
    D = D + DD

Où l'opérateur $<<<$ désigne un décalage ("rotation vers la gauche").

Ainsi, on peut résumer le procédé grâce à une suite $(\text{MD4}_i)_{0\leq i \leq k}$ et fonction de compression $h: \{0,1\}^{n+m} \rightarrow \{0,1\}^n$, qui démarre d'un IV: $\text{MD4}_0 = \text{IV},\text{MD4}_{i+1} = h(\text{MD4}_i,M_i)$. Bon… au passage, MD4 est vraiment déprécié donc Microsoft pourrait s'améliorer (oui, pas que sur cela d'ailleurs).

Conclusion

Et voilà, l'article touche à sa fin, j'espère qu'il vous aura plu et éclairé sur le sujet des fonctions cryptographiques de hachages qui peut être, à première vu, assez étrange. La cryptographie est un monde passionnant remplie de jolies applications de mathématiques, éventuellement nous nous retrouverons pour parler de courbe elliptiques qui sait ? En attendant, je vous invite à consulter les autres articles disponibles sur ilearned et ceux de mon blog !